Progressões: Progressão Geométrica

PRESSÃO HUMANA. Malthus achava que a população crescia tão rápido que logo fcaria sem alimentos. Não foi bem assim, mas o número de pessoas no mundo aumentou tanto que ameaça os recursos naturais.
Sequências que crescem ou decrescem em ritmo muito acelerado
As progressões geométricas podem explicar, pelo menos em parte, os riscos que a humanidade impõe ao meio ambiente
A história desmentiu a previsão de Malthus, de que faltariam alimentos para a população, porque ele não poderia imaginar o desenvolvimento da tecnologia. Os fertilizantes, por exemplo, aumentaram a produtividade nas lavouras. E os alimentos enlatados permitem que a população tenha o que comer mesmo em períodos de entres- safra. Mas há quem considere que as ideias do demógrafo inglês são válidas para as questões de sustentabilidade. A exploração cada vez maior de recursos naturais, como água e solo, pode levar a um colapso ecológico e econômico.
Progressão geométrica (PG) é uma sequência de números reais não nulos em que o quociente entre um termo qualquer e o termo antecedente é sem- pre o mesmo. Esse quociente constante é chamado razão da PG e é indicado por q.
Em linguagem matemática: (a1, a2, a3, a4, …, an, …) é PG desde que
![]()
No exemplo proposto por Malthus, a população, que se duplica a cada 25 anos, cresce em PG – ou seja, a cada 25 anos a população multiplica- se por 2:
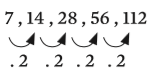
A sequência (7, 14, 28, 56, 112) é uma PG de cinco termos (n = 5) e razão q = 2, pois:
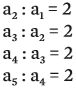
RAZÃO
Numa PA crescente, o primeiro, o quarto e o décimo terceiro termos formam uma PG. Sabendo que o primeiro termo da PA é 3, escreva a PG. A PA é (a1, a2, a3, a4, … a13)
Conhecemos a1 = 3 E, pela fórmula do termo geral de PA, sabemos que: a4 = 3 + 3 . r e a13 = 3 + 12 . r, em que r é a razão da PA (ou seja, a diferença entre dois termos subsequentes).
O enunciado diz que esses três termos formam uma PG. Tempos, portanto: (3, 3 + 3r, 3 + 12r).
A razão entre esses termos, na PG, é q – o quociente da divisão entre dois termos subsequentes: q = an / a (n-1)
A razão é sempre a mesma. Então, pode- mos igualar o quociente entre os termos a1 , a2 e a3 da PG:
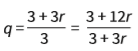
Multiplicando em cruz:
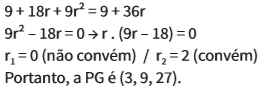
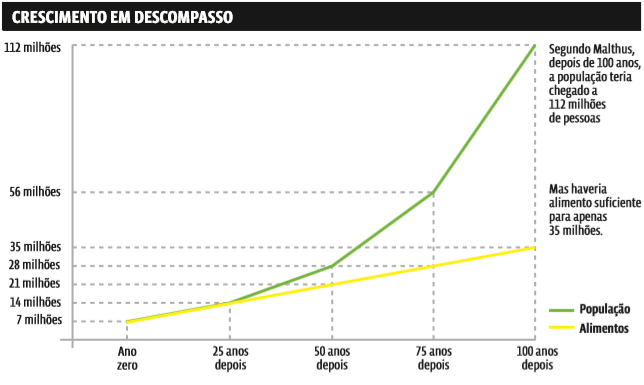
GENTE DEMAIS, COMIDA DE MENOS Acima, novamente a teoria de Malthus, agora num gráfico de linhas. Repare que, nos primeiros 25 anos, a produção de alimentos acompanharia o crescimento de uma população de 7 milhões de pessoas (ambos subiriam 7 milhões). Mas, a partir de então, a cada 25 anos, a população dobraria de tamanho e a produção de alimentos continuaria crescendo apenas 7 milhões. Ao cabo de um século, a quantidade de alimento disponível seria suficiente para apenas um terço da população.
Tipos de PG
Uma PG pode ser crescente, decrescente ou oscilante, conforme o sinal da razão (q) e do
primeiro termo (a1 ):
•Quando a1 > 0 e q > 1 ou a1 < 0 e 0 < q < 1, a PG é crescente.
A sequência (2, 6, 18, 54, 162) é uma PG crescente com a1 = 2 e q = 3.
A sequência (–5, –2,5, –1,25, –0,625) também é uma PG crescente, em que a1 = –5 e q = 0,5.
• Quando a1 › 0 e 0 ‹ q ‹ 1 ou a1 ‹ 0 e q › 1, a PG é decrescente.
A sequência (40, 20, 10, 5, …) é uma PG decrescente porque a1 = 40 e q = 0,5. A sequência (-4, -8, -16, …) também é uma PG decrescente, porque a1= -4 e q = 2.
• Quando q < 0, a PG é alternada ou oscilante – ou seja, ora o termo é negativo, ora positivo.
A sequência (4, –4, 4, –4, …) é uma PG oscilante, em que q = -1.
• Quando q = 1, a PG é constante, ou seja, todos seus termos são iguais.
Exemplos de PG constantes:
(5, 5, 5, 5, 5, …)
(1/8, 1/8, 1/8, …)
• Quando q = 0 e a1 ≠ 0, a sequência será chamada estacionária.
A PG estaciona porque qualquer número multiplicado por zero re- sulta em zero. A PG em que a1 = 5 e q = 0 é estacionária: (5, 0, 0, 0, …)
Termo geral de uma PG
Conhecendo o primeiro termo (a1) e a razão (q) de uma PG, escrevemos todos os seus demais termos.
Considere a PG ( 2, 6, 18, 54, …, an ). Nela, a1 = 2; q = 3
Acompanhe o raciocínio:
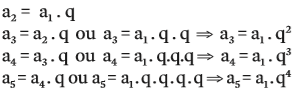
Repare que q é sempre elevada a um número que corresponde a n – 1:
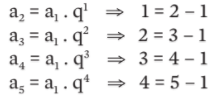
Então podemos concluir que a fórmula para o valor de qualquer termo de uma PG é dada pela expressão:
![]()
Soma dos termos de uma PG finita
Assim como fazemos com as PAs, podemos, também somar os termos de uma PG. A soma de termos de uma PG finita é dada pela seguinte expressão:
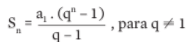

PG CRESCENTE
Determine o valor de x para que a sequência abaixo seja uma PG crescente.
![]()
Primeiro, vamos encontrar a razão q da PG:
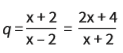
Multiplicando em cruz, temos:
![]()
Resolvendo a equação do 2º grau, obtemos dois valores para x: x1 = -2 e x2 = 6.
Substituindo esses valores na sequência confirmamos qual deles cria uma PG crescente:


TERMO GERAL
Numa PG, o terceiro termo é 50 e o sexto termo é 6 250. Qual é o primeiro termo da sequência?
Conhecemos os valores de a3 (50) e a6 (6250).
A cada termo da PG, a razão q é multiplica- da uma vez. Os dois termos dados distam três
posições (6 – 3 = 3).
Então, de um para o outro, os valores foram multiplicados pela razão q três vezes:
![]()
Conhecendo q e o valor de a3, encontramos a1.
Pelo mesmo raciocínio, entre a3 e a1, os valores foram multiplicados por q duas vezes:
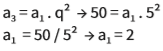









![[BF2024] - Paywall - DESKTOP - 728x90 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-DESKTOP-728x90-1.gif)
![[BF2024] - Paywall - MOBILE - 328x79 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-MOBILE-328x79-1.gif)


