Progressões: Progressão Aritmética

FALTA DE COMIDA. Para Thomas Malthus, a produção de alimentos não acompanharia o crescimento populacional.
As séries que evoluem pela soma
Numa sequência em progressão aritmética, a diferença entre dois termos é sempre a mesma
A questão da sustentabilidade é preocupação antiga. No século XIX, o demógrafo e economista inglês Thomas Malthus publicou seu mais célebre trabalho, Ensaio sobre o Princípio da População, no qual afirmava que “o poder de crescimento da população é indefinidamente maior que o poder que a Terra tem de fornecer recursos para a subsistência do homem”. Malthus comparava o ritmo de crescimento populacional com o da natureza de fornecer alimentos, por exemplo. Analisando a população da Inglaterra, à época, de 7 milhões de pessoas, e a produção das lavouras, ele concluiu que rapidamente o campo não teria mais condições de alimentar todos.
A defasagem entre o crescimento da população e o aumento da produção de alimentos, pela ideia de Malthus, ocorreria porque o primeiro, para ele, seguia uma progressão geométrica (PG), e o segundo, uma progressão aritmética (PA). Aqui você conhece as PAs.
Progressão aritmética (PA) é uma sequência de valores (ou termos) em que a diferença (ou razão, r) entre um termo qualquer e seu antecedente é sempre a mesma, ou seja, é constante. Em linguagem matemática:
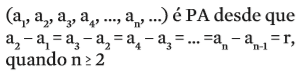
É o que ocorre com o ritmo de aumento na produção de alimentos no exemplo proposto por Malthus. A cada 25 anos, a quantidade de alimentos aumenta, mas ainda é suficiente para alimentar mais 7 milhões de pessoas, apenas:
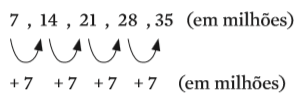
Dizemos que a sequência (7, 14, 21, 28, 35) é uma PA em que n = 5 e r = 7. Ou seja, é uma sequência de cinco valores que variam seguindo a razão 7, pois:
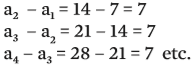
Tipos de PA
Uma PA pode ser crescente, decrescente ou constante, dependendo do valor da razão:
- Se r > 0, a PA é crescente. A sequência (-6, -1, 4, 9, …) é uma PA crescente, porque r = 5;
- Se r < 0, a PA é decrescente. A sequência (23, 20, 17, 14, …) é uma PA decrescente porque r = -3;
- Se r = 0, então todos os termos da PA serão iguais. A PA é constante. A sequência (5, 5, 5, …) é uma PA constante porque r = 0.
Termo geral de uma PA
Podemos escrever todos os termos de uma PA conhecendo apenas:
- – o primeiro termo e a razão da PA; ou
- – dois termos e suas posições na sequência.Considere a PA abaixo, em que r = 5:
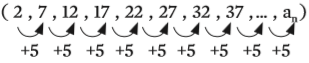
É possível deduzir o valor de um termo qualquer (an) descobrindo a lei matemática que define cada termo da PA:
![]()
Da mesma maneira:
![]()
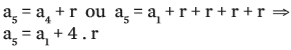
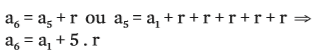
Repare que o fator que multiplica r vale sempre n – 1:
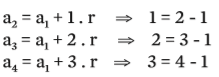
Então, podemos concluir que a fórmula para calcular o valor de qualquer termo da PA é:
Soma de termos de uma PA
Em toda PA finita, a soma de quaisquer dois termos equidistantes dos extremos é igual à soma dos extremos. Observe:
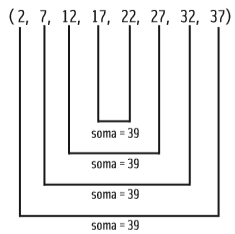
Com a propriedade acima, podemos calcular a soma de todos os termos de uma PA finita.
Na PA (2, 7, 12, 17, 22, 27, 32, 37), já calculamos a soma de dois termos equidistantes dos extremos: 39. Para a soma de todos os oito termos (S8), temos, então:

Repare que, como os termos foram somados aos pares, para uma PA de oito termos, temos quatro pares. Então, podemos definir a regra para a soma total dos termos de uma PA:
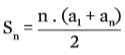
Com a mesma expressão, calcula-se a soma dos n primeiros termos de uma PA. Veja:
Se na PA (2, 7, 12, 17, 22, 27, 32, 37) quisermos calcular a soma dos quatro primeiros termos (S4), recorreremos de novo à soma dos termos equidistantes dos extremos:
2 + 17 = 19
7 + 12 = 19
Então, S4= 2 .19 = 38
Confira com a fórmula:
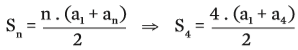
![]()
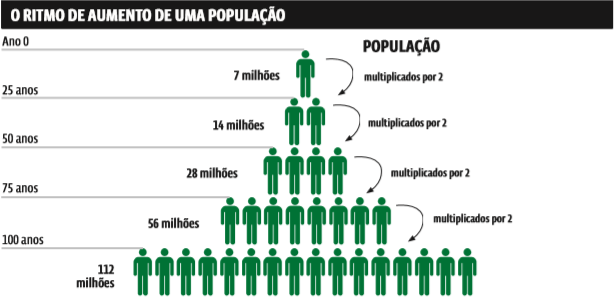

O RACIOCÍNIO DE MALTHUS A primeira pirâmide mostra o crescimento da população da Inglaterra, à época dele, de 7 milhões de habitantes; a segunda, o aumento na produção de alimentos. A população dobra de tamanho a cada período de 25 anos. Já a produção de alimentos cresce sempre em PA – pela soma de 7 milhões a cada período de 25 anos: 7 + 7 + 7… A história acabou desmentindo Malthus. O desenvolvimento tecnológico aumentou a produtividade das fazendas. E a industrialização permite estocar alimentos por longos períodos, aumentando a oferta para a população

TERMO GERAL E SOMA DOS TERMOS DE UMA PA
Quantos múltiplos de 3 existem entre 100 e 299?
A sequência de múltiplos é uma PA. Neste caso, uma PA de r = 3 (a diferença entre 3, 6, 9,…). O primeiro e o último termo têm de ser divisíveis por 3. Então, a1 = 102 e an = 297.
an = 297 é o último termo da sequência. Pela fórmula para o termo geral de PA, temos:
an = a1 + (n – 1) . r → 297 = 102 + (n – 1) . 3 → 195 = 3n – 3 → 198 = 3n → n = 66
Existem, portanto, 66 múltiplos de 3 no intervalo de 100 a 299.
Qual o valor de x que torna verdadeira a equação (x – 3) + (x – 6) + (x – 9) + … + ( x – 42) = 371?
O lado esquerdo da equação traz uma PA em que a1 = (x – 3), a2 = (x – 6) … an = (x – 42)
A razão dessa PA é r = a2 – a1 = (x – 6) – (x – 3) = x – x – 6 + 3 → r = -3
Então, a1 = x – 3 e an = x – 42
O valor de n para o último termo, pela fórmula do termo geral é:
an = a1 + (n – 1) . r → x – 42 = (x – 3) + (n – 1) . (-3) = x – 3 – 3n + 3 → 3n = 42 → n = 14
Encontramos o valor de x, usamos a fórmula para a soma de termos: Sn = n . (a1 + an) / 2
S14 = 14 . [(x – 3) + (x – 42)] / 2 → S14 = 14 . (2x – 45) / 2 → S14 = 14 . x – 315
Voltando à equação original, temos então 14x – 315 = 371 → x = 371 + 315 / 14 → x = 49








![[BF2024] - Paywall - DESKTOP - 728x90 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-DESKTOP-728x90-1.gif)
![[BF2024] - Paywall - MOBILE - 328x79 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-MOBILE-328x79-1.gif)


