Cinemática: Conceitos

AINDA ASSIM, MOVE-SE. O ônibus está em movimento em relação à rua. Mas dentro dele os passageiros estão parados uns em relação aos outros.
O que define um movimento
A cinemática é o ramo da física que estuda o movimento dos corpos em geral – tanto de um atleta que corre, nada ou salta quanto de um foguete que deixa a superfície da Terra, ou de um corpo que circula em órbita do planeta. A cinemática não se preocupa com a causa do movimento, apenas com o movimento em si. Com ela somos capazes de determinar a posição, a velocidade e a aceleração do corpo no decorrer do tempo. Neste capítulo, você conhece os conceitos básicos com que lida a cinemática.
REFERENCIAL
Imagine que você esteja viajando em um trem. Você está em repouso ou em movimento? Se essa pergunta é feita a uma pessoa que se encontra parada ao lado da estrada de ferro, você está em movimento. Porém, se a mesma pergunta se dirige a outro passageiro do mesmo trem, você está em repouso. Ou seja, a noção de movimento ou repouso de certo objeto móvel não depende apenas do objeto, mas do corpo que adotamos como referência do movimento. Tal corpo que utilizamos para analisar se o móvel está ou não em movimento chamamos de referencial ou sistema de referência.
Dizemos que um móvel qualquer está parado ou em repouso quando sua posição não varia em relação a determinado referencial. O objeto móvel está em movimento quando sua posição varia em relação a determinado referencial. Um mesmo objeto pode estar em repouso em relação a um referencial e em movimento em relação a outro. O termo “em relação”, repetido nas frases acima, indica que o movimento é relativo: suas medidas dependem dos referenciais adotados.
DIMENSÕES DO CORPO
O tamanho de um corpo em relação às demais dimensões envolvidas no movimento pode ser importante para os cálculos. Quando não podemos desprezar as dimensões do corpo em relação às demais dimensões, dizemos que esse é um corpo extenso. É o caso de um trem de 50 metros de comprimento que se desloca por 100 metros.
Em outros casos, as dimensões do corpo estudado são tão menores que as demais dimensões envolvidas no movimento que podemos tratar o corpo como um ponto material. A Estação Espacial Internacional (ISS) é um exemplo de ponto material. A ISS é grande – tem cerca de 100 metros de ponta a ponta. Mas fica minúscula se comparada ao percurso de dezenas de milhares de quilômetros que faz em torno da Terra.


O PONTUAL E O EXTENSO. A estação espacial é um ponto se comparada à sua trajetória ao redor da Terra. Já um automóvel que manobra em poucos metros não pode ter suas dimensões desprezadas.
CENTRO DE MASSA
Podemos explicar os movimentos de um corpo extenso e as forças que atuam sobre ele utilizando o conceito de centro de massa (CM) – o ponto no qual se considera que toda a massa do corpo esteja concentrada. O CM se movimenta como se todas as forças externas que atuam sobre o corpo fossem aplicadas sobre ele.
No caso de um corpo rígido e homogêneo – ou seja, que não se deforma e que é constituído de um mesmo material e com a massa distribuída de maneira uniforme –, o CM coincide com o centro de gravidade (CG) – aquele no qual a força peso está concentrada. E, em corpos de formato regular, ambos coincidem com o centro geométrico. Veja:

Uma folha de papel pode ser considerada um corpo bidimensional. Nesse caso, o CM e o CG ficam no centro geométrico do retângulo.

Num corpo tridimensional, rígido e homogêneo, como um dado não viciado, o CM coincide com o CG, exatamente no centro do cubo.

O CM pode estar fora do corpo e, ainda assim, coincidir com o CG.
TRAJETÓRIA
Dizer que o movimento de um corpo é relativo implica dizer que sua trajetória é relativa, ou seja, o caminho percorrido pelo corpo em determinado tipo de movimento depende do referencial adotado.
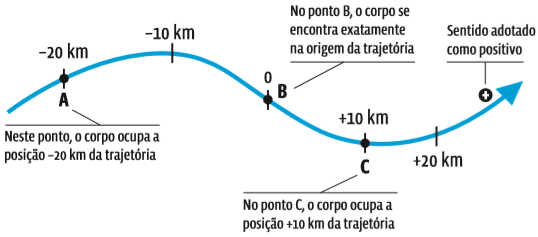
Para estudar um corpo que descreve uma trajetória em relação a determinado referencial escolhemos uma origem, ou seja, um ponto a partir do qual as posições ocupadas pelo corpo serão registradas e contadas.
Definimos, em seguida, um sentido para essa trajetória. Assim, podemos identificar o sentido em que as posições ocupadas pelo corpo crescem ou diminuem (veja o quadro Como a posição muda, ao lado).
DESLOCAMENTO ESCALAR
Ao se deslocar, um corpo assume diferentes posições ao longo da trajetória. Essa variação de posições é chamada deslocamento escalar (ΔS). A medida do deslocamento escalar é obtida pela diferença entre a posição final e a posição inicial de um corpo após percorrer um trecho qualquer. Matematicamente:
![]()
Na figura Como a posição muda, ao lado, o objeto que parte do ponto B e ao final do percurso atinge o ponto C tem deslocamento escalar dado pela expressão:
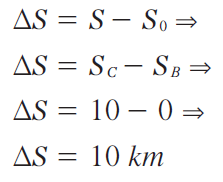
Mas, se o móvel partir do ponto C e atingir ao final da viagem o ponto A, seu deslocamento será de:

Repare que o deslocamento, neste caso, é negativo. Isso indica que o percurso foi realizado no sentido contrário ao adotado como positivo na trajetória.
TIPOS DE MOVIMENTO
Um movimento é classificado conforme seu deslocamento ao longo da trajetória. Movimentos progressivos são aqueles nos quais o deslocamento se dá no sentido adotado como positivo na trajetória. Assim, num movimento progressivo, o deslocamento escalar de um corpo é positivo.

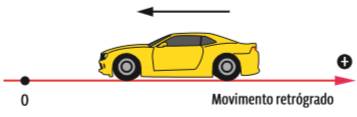
Movimentos retrógrados são aqueles cujo deslocamento acontece no sentido inverso ao adotado como positivo na trajetória. Num movimento retrógrado, o deslocamento escalar de um corpo é negativo.
VELOCIDADE ESCALAR MÉDIA
É a razão entre o deslocamento escalar (∆S) descrito por um corpo e o intervalo de tempo (∆t) gasto nesse deslocamento. Ou seja, é a variação da posição ocupada por um corpo em determinada trajetória no decorrer do tempo. Matematicamente:
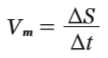
Os corpos que descrevem movimentos progressivos apresentam velocidades positivas (v > 0), enquanto corpos que descrevem movimentos retrógrados apresentam velocidades negativas
(v < 0). No S.I., a unidade de medida para velocidade é metro por segundo (m/s).
ACELERAÇÃO ESCALAR MÉDIA
É a medida da variação da velocidade do corpo em certo intervalo de tempo. Matematicamente:
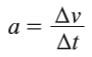
A aceleração de um móvel pode ser entendida como a velocidade com que varia a sua velocidade. No S.I., a unidade de medida utilizada para a aceleração é m/s2.
GRANDEZAS ESCALARES E VETORIAIS
Algumas grandezas necessitam apenas de seu valor absoluto para ser caracterizadas. São as grandezas escalares, como tempo, volume e massa. Outras grandezas exigem que sejam defnidos também sua direção e seu sentido. Essas são grandezas vetoriais – aquelas nas quais um vetor indica a intensidade, a direção e o sentido. São grandezas vetoriais a velocidade, a aceleração e a força, por exemplo.
Veja abaixo como é indicada a velocidade de um objeto:
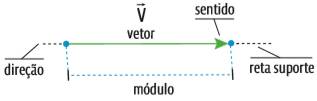
Módulo é a medida pura do comprimento do vetor (indica a intensidade da velocidade)
Direção é dada pela direção da reta suporte em que o vetor se encontra
Sentido é definido pela ponta da seta
SOMA DE VETORES
As grandezas escalares podem ser somadas algebricamente: num bolo, 1 kg de açúcar mais 2 kg de farinha resultam em 3 kg de ingredientes. Mas a soma vetorial precisa considerar, além do módulo, a direção e o sentido dos vetores.
Existem dois métodos geométricos para a adição de vetores. O primeiro, o método da poligonal. Nele, a origem do segundo vetor coincide com a extremidade (ponta da fecha) do primeiro vetor. O vetor soma (ou resultante) é o vetor que fecha o polígono, com origem no mesmo ponto de origem do primeiro vetor.
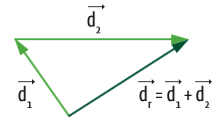
A mesma ideia pode ser usada para a soma de mais de dois vetores. Veja:

O segundo método para somarmos vetores, dois a dois, é o do paralelogramo: fazemos coincidir as origens dos dois vetores e construímos um paralelogramo. O vetor soma é a diagonal do paralelogramo cuja origem coincide com a dos dois vetores. Veja:
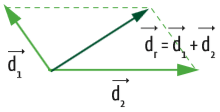
SOMA DE VETORES
Nesta trajetória, todas as posições são definidas a partir do ponto B, e o sentido adotado é da esquerda para a direita.
Deslocamento escalar e distância percorrida são grandezas diferentes. Veja a comparação das duas para um objeto que sai do ponto A, segue até o ponto C e volta para o ponto B.
A distância percorrida é a soma de todos os trechos percorridos, não importando o sentido da viagem. Então:

![]()
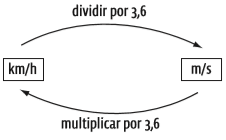
CONVERSÃO DE ESCALAS
Para converter quilômetros por hora (km/h) em metros por segundo (m/s), basta transformar cada uma das unidades:
– 1 km = 1 000 m
– 1 hora tem 60 minutos, cada um deles com 60 segundos. Então, 1 h = 60 s . 60 s = 3 600 s
Assim,
![]()
Para transformar m/s em km/h, é só fazer o raciocínio inverso:
![]()
Um automóvel parte de uma cidade localizada no quilômetro 100 de uma estrada, às 10 horas. E chega à cidade vizinha, no quilômetro 244, às 12 horas. A velocidade média do automóvel no trajeto percorrido foi de:

![]()
Um objeto que apresenta uma aceleração de 2 m/s2 tem a intensidade de sua velocidade aumentada em 2 m/s a cada segundo. Já um objeto que apresenta uma aceleração negativa, por exemplo, –3 m/s2, tem a intensidade de sua velocidade diminuída em 3 m/s a cada segundo.









