Trigonometria: Triângulos e circunferência

ESCALA DA POLUIÇÃO. Engenheiros associam cores e trigonometria para avaliar o volume de petróleo vazado de uma plataforma marítima.
A circunferência trigonométrica facilita os cálculos que envolvem ângulos de triângulos retângulos
O triângulo e suas medidas são úteis em diversas áreas do conhecimento, além do cálculo de alturas e altitudes. Na arquitetura, para definição de dimensões como altura de um edifício; na cartografa, para o desenho, em escala, de mapas; e na astronomia, para cálculo de distâncias e posições relativas dos astros.
As relações entre as medidas dos lados e dos ângulos de triângulos retângulos são úteis, também, para engenheiros ambientais. No caso de um vazamento de petróleo em mar, por exemplo, é possível usar a relação entre ângulos de um triângulo na avaliação do volume vazado, com fotos batidas de satélites ou aviões. O óleo vazado adquire tonalidades mais escuras e mais claras, conforme a espessura da camada sobre a água. Os engenheiros conhecem a relação entre tom e espessura. Assim, avaliando a área correspondente a cada tom, fica fácil medir o volume total.
A partir daí entra a trigonometria: a área captada pela foto é proporcional à área real da mancha, no mar. O cálculo dessa proporção envolve conceitos como semelhança de triângulos e relações trigonométricas.
Triângulos semelhantes
Dois triângulos são semelhantes quando seus ângulos e lados correspondentes mantêm uma razão de proporção. Ângulos correspondentes são aqueles que ocupam a mesma posição em relação aos lados de um triângulo. Lados correspondentes são aqueles que ocupam a mesma posição em relação aos ângulos. Então, em triângulos semelhantes os ângulos e lados correspondentes são proporcionais. Por consequência, as áreas dos triângulos também são proporcionais.
Acompanhe o raciocínio observando a figura abaixo:
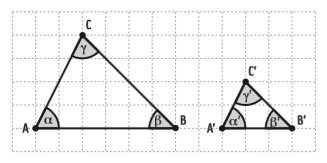
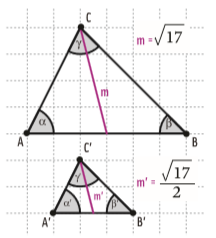
É fácil perceber que os triângulos ABC e A’B’C’ são parecidos. Eles são triângulos semelhantes por duas razões:
- • Seus ângulos correspondentes são congruentes (têm medida igual). Na figura, o ângulo α é correspondente de α’, β é correspondente de β’ e γ, de γ ’.
- • Seus lados correspondentes são proporcionais. Na figura, você observa:
- → o lado AC é correspondente de A’C’
- → o AB é correspondente de A’B’
- → o lado BC é correspondente de B’C’.
Razão de semelhança
Ainda observando os dois triângulos, repare que o lado AB mede 6 unidades (6 quadradinhos). E seu correspondente A’B’ mede 3 unidades. A razão de semelhança entre esses lados correspondentes, então, é
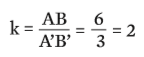
A razão se mantém para os demais pares de lados correspondentes:
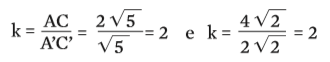
Dizemos, então, que o triângulo AB está para A’B’ na escala de 2 para 1 (em notação matemática, 2 : 1). É esse tipo de escala que permite que se mantenham as proporções em mapas – e que se saiba com bastante precisão o real tamanho da mancha de petróleo no Golfo do México.
Triângulos semelhantes também têm áreas semelhantes. Se a razão de semelhança entre os lados vale k, a razão entre as áreas é k2.
A razão de semelhança se mantém também para as demais medidas lineares do triângulo. Entre alturas:
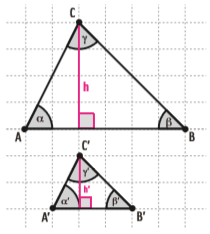
![]()
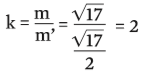
Triângulos semelhantes sempre têm três ângulos congruentes. Acompanhe na figura abaixo o que acontece quando essa semelhança ocorre entre dois triângulos retângulos (aqueles que têm um ângulo de 90°):
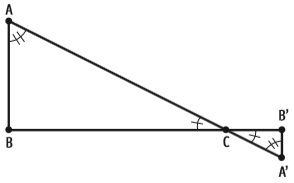
Veja que os triângulos ABC e A’B’C têm um ângulo de 90° (em B e B’).
Os dois também têm um vértice em comum (C). Então, os ângulos definidos por esse vértice em cada triângulo são congruentes.
A soma dos ângulos internos de um triângulo é 180°. Então, se os dois primeiros ângulos são congruentes, o último também será congruente. Conclusão: os triângulos ABC e A’B’C são semelhantes.
A trigonometria é uma ferramenta para calcular medidas e proporções entre triângulos retângulos. A base para isso é a circunferência trigonométrica.
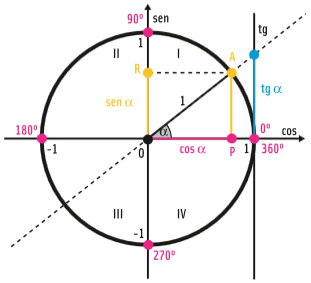
Observe que:
- • A circunferência é desenhada sobre um plano cartesiano (eixos x e y);
- • O eixo x corresponde à medida do cosseno (cos);
- • O eixo y corresponde à medida do seno (sen);
- • O centro da circunferência está sobre o ponto O, de coordenadas (0,0);
- • O raio da circunferência é uma unidade;
- • O segmento em azul é a tangente do ângulo α (tg α);
- • A circunferência é dividida em quatro quadrantes (I, II, III, e IV);
- • Os graus são lidos a partir da direita, no sentido anti-horário: 0°, 90°, 180°, 270° e 360°.
Podemos desenhar na circunferência ângulos de 0° a 360° e obter o valor das razões trigonométricas. Acompanhe atentamente na figura:
- • O segmento OA é a hipotenusa de um triângulo retângulo formado pelos pontos OAP;
- • O raio da circunferência é uma unidade. Então, o segmento OA (a hipotenusa) vale uma unidade;
- • A hipotenusa forma com o lado positivo do eixo x um ângulo α;
- • O ponto A tem coordenadas (x, y). O o eixo x é o eixo dos cossenos e o y, eixo dos senos. Então, as coordenadas de um ponto qualquer A são (cos α, sen α). Esta relação vale para qualquer ponto da circunferência.
Os quadrantes
Dependendo do quadrante em que o ponto A se encontra, os valores do seno, cosseno e tangente serão positivos ou negativos. Acompanhe:
Quando o ponto A está no quadrante I, o ângulo α terá valor entre 0° e 90°. Veja que, nessa faixa de ângulos, todos os valores de x e y são positivos. Portanto, o seno, o cosseno e a tangente de ângulos no quadrante I são positivos. E os valores do seno, do cosseno e da tangente serão positivos:
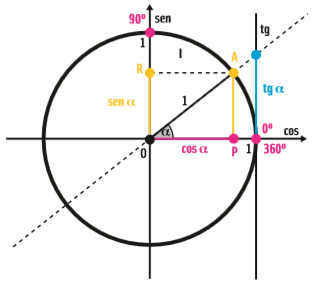
Se o ponto A estiver no quadrante II, o ângulo α terá como medida um valor entre 90° e 180°. Veja na figura abaixo: o valor de y (seno) é positivo, mas x (cosseno) é negativo; a tangente, portanto, também é negativa:
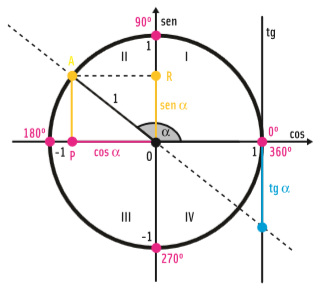
Para um ponto A que esteja no quadrante III, o valor de α ficará entre 180° e 270°. O seno e o cosseno serão negativos. A tangente será positiva:
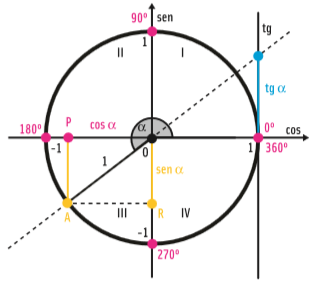
Finalmente, para um ponto que esteja no quadrante IV, α estará entre 270° e 360°. Nesse caso, o cosseno é positivo e o seno e a tangente, negativos:
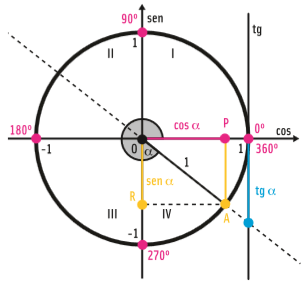
Pitágoras e a trigonometria
Se aplicarmos o Teorema de Pitágoras num triângulo desenhado no 1° quadrante da circunferência trigonométrica, teremos:
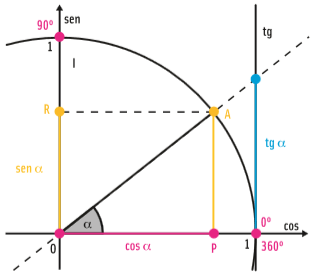
- • Os dois catetos do triângulo AOP são os valores de seno e cosseno do ângulo α;
- • A hipotenusa, que é o raio da circunferência trigonométrica, tem medida 1.
Então sen2 α + cos2 α = 1
Esta é a chamada relação fundamental da trigonometria.
Ainda no triângulo AOP, podemos calcular a tangente do ângulo α e obter outra relação:
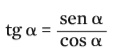
Razões trigonométricas em um triângulo retângulo
Com a trigonometria, estabelecemos as razões de semelhança entre triângulos retângulos, associando a medida dos lados à circunferência trigonométrica.
As razões trigonométricas são definidas com base nas relações entre as medidas dos lados do triângulo e têm como referência os ângulos.

Simetria na circunferência trigonométrica
Podemos calcular o valor para um ângulo α de qualquer quadrante trabalhando apenas com ângulos do quadrante I. É que qualquer ponto da circunferência tem três pontos simétricos em relação aos eixos cartesianos nos outros três quadrantes. Veja:
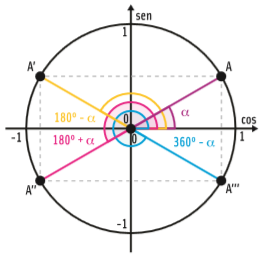
Os pontos A, A’, A’’ e A’’’ são simétricos em relação aos eixos cartesianos. Traduzindo: as coordenadas desses pontos têm os mesmos valores absolutos. A única diferença são os sinais, que variam conforme o quadrante. Portanto, os ângulos definidos por esses pontos têm seno e cosseno iguais, só variando os sinais, conforme o quadrante.
Essa simetria é muito útil quando precisamos trabalhar com triângulos que contenham um ângulo maior que 90°.
Ângulos complementares e suplementares
Ângulos complementares são dois ângulos (α e β) que, somados, resultam em 90°. Ângulos complementares apresentam algumas propriedades:
Se α + β = 90°, então:
- • sen α = cos β
- • cos α = sen β
- • tg α = 1/tg β
Os ângulos α e β são suplementares quando sua soma resultar em 180°.
Se α + β = 180°, então:
- • sen α = sen β
- • cos α = –cos β
- • tg α = –tg β
Lei dos senos e cossenos
Para triângulos que não são retângulos (chamados acutângulos ou obtusângulos), duas outras relações são muito importantes. São as leis dos senos e dos cossenos.
Observe o triângulo obtusângulo abaixo:
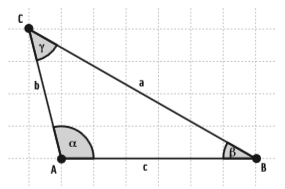
A lei dos senos estabelece que:
![]()
E a lei dos cossenos, que:
![]()
Repare que, nesta formulação, α é o ângulo oposto ao lado a. Da mesma maneira, podemos estabelecer a lei dos cossenos para os demais ângulos:
b2 = a2 + c2 – 2 . a . c . cos β , em que β é o ângulo oposto ao lado b;
c2 = a2 + b2 – 2 . a . b . cos γ , em que γ é o ângulo oposto ao lado c.
Num triângulo qualquer, a razão entre a medida de um lado e o seno do ângulo oposto a esse lado tem valor igual ao diâmetro da circunferência que circunscreve o triângulo. O diâmetro é d = 2 . r
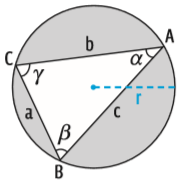
Então, na lei dos senos, temos que
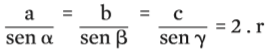

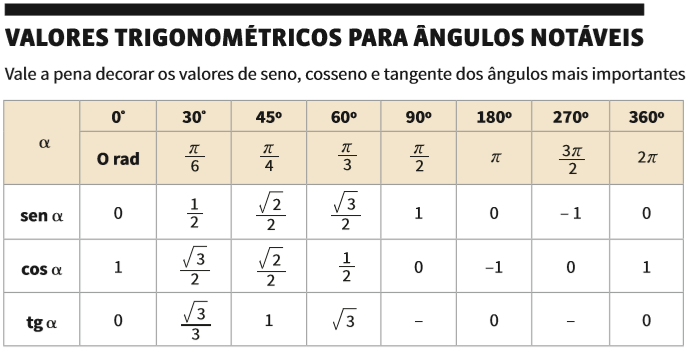
RELAÇÕES TRIGONOMÉTRICAS
Considere o triângulo retângulo ABC, abaixo, de catetos medindo 4 e 6 unidades e o ângulo reto em C. Qual a medida dos ângulos α e β?
Dados:
Desenhando a situação descrita:
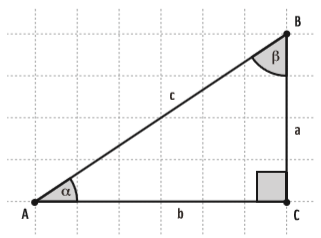
Por Pitágoras, encontramos o valor da hipotenusa (c):
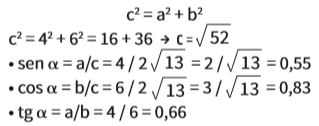
Existe um único ângulo que combina esses valores de seno, cosseno e tangente. Consultando uma tabela de valores trigonométricos, ou utilizando uma calculadora científica, descobrimos que α mede, aproximadamente, 34°.
Os três ângulos internos de um triângulo somam 180°. Um desses ângulos mede 90°; outro, 34°. Então, o terceiro ângulo (β) mede: 180° – 90° – 34° + β = 56°.

ÂNGULOS MAIORES QUE 360°
Calcule o seno, o cosseno e a tangente do ângulo de 1 230°.
O ângulo de 1 230° é bem maior que os 360° de uma volta completa na circunferência. Para verificar essa diferença no tamanho, dividimos 1 230 por 360:
1 230 : 360 = 3,41…
Então, 1 230° correspondem a mais de três voltas na circunferência.
Três voltas na circunferência são 360° . 3 = 1080°
Quanto falta ainda para chegar aos 1 230°? 1 230 – 1 880 = 150°
Então, o seno, o cosseno e a tangente de 1 230° são iguais ao seno, ao cosseno e à tangente de 150°.
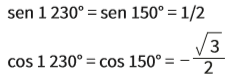
A tangente é calculada dividindo-se o seno pelo cos:
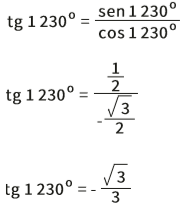








![[BF2024] - Paywall - DESKTOP - 728x90 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-DESKTOP-728x90-1.gif)
![[BF2024] - Paywall - MOBILE - 328x79 (1)](https://gutenberg.guiadoestudante.abril.com.br/wp-content/uploads/sites/4/2024/11/BF2024-Paywall-MOBILE-328x79-1.gif)


